Atomic congestion games with non-separable costs: an application to smart charging

Mar 12 14:00 ₂₀₂₄

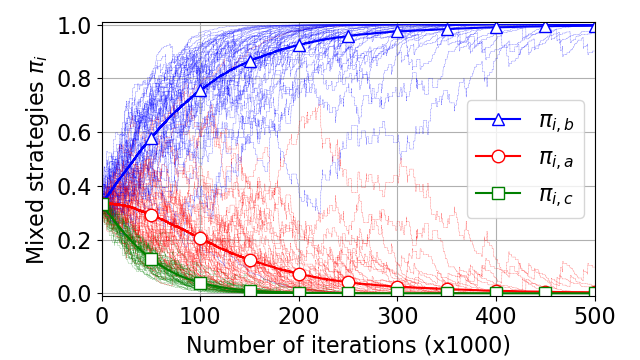
Abstract: Atomic congestion games with separable costs are a specific type of non-cooperative games with a finite number of players where the cost of a commodity depends on the number of players choosing it. But in many applications, resources may be correlated in the sense that the resource cost may depend on the usage of other resources, and thus cost function is non-separable. This is the case for traffic models with opposite directions dependencies, resource graph games, and smart charging games to cite a few examples. In this talk, after introducing the concepts of atomic congestion games with non-separable costs, a specific smart charging game will illustrate such game theoretical framework. In this particular setting, we prove the existence of pure Nash Equilibrium by showing ordinal potential function existence. We also demonstrate the convergence of a simple Reinforcement Learning algorithm to the pure NE for both synchronous and asynchronous versions. Finally, the recent framework of Resource Graph Games will be presented. In this setting, dependencies between resources are modeled as an oriented graph. This new framework generalizes atomic congestion games with non-separable costs and opens new questions about the existence and uniqueness of pure NE in this general setup.